벡터화, 배치 경사 하강법

지금까지 단일 신경층망을 구현해보았는데 이제는 단일층이 아닌 2개의 층을 가진 신경망을 구현해보고자 한다.
그 전에 신경망 알고리즘을 벡터화 하는 것에 대해 알아보자.

신경망 알고리즘을 벡터화하여 한 번에 전체 샘플을 사용

이전에 사용한 데이터 세트 즉 사이킷런의 예제 데이터 세트는 2차원 배열로 저장되어있었다.
머신러닝에서는 훈련 데이터를 이와같이 2차원 배열로 표현하는 경우가 많다.
2차원 배열은 행은 샘플이고, 열은 특성으로 이루어져 있었고 이것을 행렬로 볼 수 있다.

이러한 행렬 개념을 신경망 알고리즘에 도입해 보려고 한다.

벡터화된 연산은 알고리즘의 성능을 올림

넘파이, 머신러닝, 딥러닝 패키지들은 다차원 배열의 계산을 빠르게 수행할 수 있다는 특징을 가지고 있다.
이 말은 곧 행렬 연산을 빠르게 수행할 수 있다는 말과 같다.
-> 이러한 기능을 벡터화(vectorization)된 연산이라고 한다
이렇게 벡터화되 연산을 사용하면 알고리즘의 성능을 높일 수 있다.

그러면 이전에 구현한 SingleLayer 클래스에 어떻게 벡터화된 연산을 적용할 수 있을까??
-> 배치 경사 하강법을 SingleLayer 클래스에 적용하면 벡터화된 연산을 사용할 수 있습니다.

배치 경사 하강법으로 성능을 올림

배치 경사 하강법이 무엇이지 ???
지금까지 사용한 경사 하강법 알고리즘들(선형 회귀, 로지스틱 회귀)은 알고리즘을 1번 반복할때 1개의 샘플을 사용하는 확률적 경사 하강법을 사용했다.
SingleLayer 클래스에도 확률적 경사 하강법을 사용했었다.
확률적 경사 하강법은 가중치를 1번 업데이트 할 때 1개의 샘플을 사용하므로 손실 함수의 전역 최솟값을 불안정하게 찾는다.
하지만 배치 경사 하강법은 가중치를 1번 업데이트할 때 전체 샘플을 사용하므로 손실 함수의 전역 최솟값을 안정적으로 찾는다.
단 배치 경사 하강법은 가중치를 1번 업데이트할 때 사용되는 데이터의 개수가 많으므로 알고리즘 1번 수행당 계산 비용이 많이 든다.
-> 그래서 전체 데이터 세트의 크기가 너무 크면 배치 경사 하강법을 사용하지 못하는 경우가 있다.

이제부터 배치 경사 하강법을 사용하기 위해 벡터화된 연산의 기초에 대해 알아보려고 한다.

벡터 연산과 행렬 연산

벡터화된 연산을 제대로 사용하기 위해선 벡터 연산과 행렬 연산을 알아야 한다.
여기에서는 신경망에서 자주 사용되는 벡터 연산 중 하나인 점 곱(스칼라 곱)과 행렬 곱셈에 대해 알아볼 것이다

스칼라 곱(점 곱)

단일층 신경망을 그림으로 나타내면 아래와 같다.

단일층 신경망에서 z를 구했던 방법은 가중치($w_1, w_2$, …)와 입력 ($x_1, x_2$, …)을 각각 곱하여 더했다. 여기다 절편도 더한다.
이 계산을 이전에 만든 SingleLayer 클래스 안에 forpass()에서

z = np.sum(x * self.w) + self.b

로 구현하였다.
위 식에서 입력 가중치의 곱을 x * self.w로 간단하게 표현할 수 있는 이유는 넘파이의 원소별 곱셈 기능 덕분이다.
정확히는 아래와 같은 원리로 가중치와 입력의 곱에 대한 합을 한번에 계산한 것이다.

x = [x_1, x_2, ..., x_n]
w = [w_1, w_2, ..., w_n]

x * w = [x_1 * w_1, x_2 * w_2, ..., x_n * w_n]

여기서 x(x_1, x_2, …)와 w(w_1, w_2, …)를 벡터라고 부른다
그리고 위의 두 벡터를 곱하여 합을 구하는 계산 (np.sum(x * welf.w)) 를 스칼라 곱(점 곱(dot product)) 라고 한다.

벡터 a, b에 대한 점 곱은 $a \cdot b$로 표현한다.

아래 그림은 단일층 신경망에 점 곱을 적용하여 다시 그린 것이다.

점 곱을 행렬 곱셈으로 표현합니다.

점 곱을 행렬 곱셈으로 표현하면 행방향으로 놓인 첫 번째 벡터와 열 방향으로 놓인 두 번째 벡터의 원소를 각각 곱한 후 모두 더한는 것과 같다.
아래 식을 보면 행렬 곱셈 방식을 알 수 있다.
$XW = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix} \begin{bmatrix} w_1 \ w_2 \ w_3 \end{bmatrix} = w_1 \times x_1 + w_2 \times x_2 + w_3 \times x_3$

$x_1$은 $w_1$, $x_2$는 $w_2$, $x_3$는 $w_3$와 곱하여 모두 더한다.

이저네 본 np.sum(x * self.w)의 계산과 정확하기 일치한다.
행렬의 곱셈을 계산하는 넘파이의 np.dot() 함수를 이용하면 np.sum(x * self.w)를 아래와 같이 나타낼 수도 있다.

z = np.dot(x, self.w) + self.b

위 행렬의 곱셈 원리를 훈련 데이터의 전체 샘플에 대해 적용하면 배치 경사 하강법을 구현할 수 있다.

전체 샘플에 대한 가중치 곱의 합을 행렬 곱셈으로 구함

이제 이전에 설명한 것을 이용하여 훈련 데이터의 전체 샘플에 대한 가중치 곱의 합을 행렬 곱셈으로 표현해 볼것이다.
훈련 데이터의 샘플은 각 샘플이 하나의 행으로 이루어져 있다.
따라서 행렬 곱셈을 적용하면 샘플의 특성과 가중치를 곱하여 더한 행렬을 얻을 수 있다.

행렬의 곱셈의 결과 행렬의 크기는 첫 번째 행렬의 행과 두 번쨰 행렬의 열이 된다.
식으로 보면
$(m, n) \cdot (n, k)$ = (m, k)
즉 첫 번째 행렬의 행 크기 m과 두번쨰 행렬의 열 크기 k가 행렬의 곱셈의 결과인 행렬의 크기 (m, k)가 된다.

또한 행렬의 곱셈이 가능하려면 첫 번쨰 행렬의 열의 크기와 두번쨰 행렬의 행의 크기가 같아야 한다.
위의 식을 보면 첫 번째 행렬의 열의 크기와 두번째 행렬의 행의 크기가 둘다 n으로 같음을 알 수 있고 이 조건을 만족해야만 행렬의 곱셈이 가능하다.

첫번째 행렬 x, 두번째 행렬 w가 있다면 위 조건만 만족하면 크기가 어떻든 행렬의 곱셈이 가능하고
이전에 보았듯 행렬의 곱셈은 넘파이의 np.dot() 함수를 이용하면 간단히 계산이 된다.
아래 코드를 보자

np.dot(x, w)

이제부터 행렬 연산을 사용해서 SingleLayer 클래스에 배치 경사 하강법을 적용해 볼 것이다.

# SingleLayer 클래스에 배치 경사 하강법을 적용해보자

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer # 위스콘신 유방암 데이터 이용

from sklearn.model_selection import train_test_split

cancer = load_breast_cancer()

x = cancer.data
y = cancer.target

x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify = y, test_size = 0.2, random_state = 42)

x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify = y_train_all, test_size = 0.2, random_state = 42)

# cancer 데이터 세트의 특성 개수는 30개 이다. 그래도 시작하기전에 사용할 데이터의 크기를 확인하는 습관을 가지는 것이 좋다.
print(x_train.shape, x_val.shape)

# 훈련 데이터 세트 샘플은 364개 이고, 특성 개수는 30개 임을 알 수 있다.

(364, 30) (91, 30)

위 예제의 정방향 계산을 행렬 곱셈으로 표현해 보자

넘파이를 사용하면 절편을 더하는 계산을 위해 (364, 1) 크기의 행렬을 따로 만들 필요가 없다.
행렬에 스칼라 값을 더하면 자동으로 행렬의 각 요소에 스칼라 값을 더해 주기 때문이다.
위 식을 보면 벡터와 스칼라의 덧셈 연산을 알 수 있을 것이다.

gradient 계산을 이해해보자

방금 정방향 계산을 구하는 방법을 알아보았는데 gradient를 갱신하기 위한 gradient를 어떻게 계산할 수 있을까?
gradient는 오차와 입력 데이터의 곱이므로 다음과 같은 행렬 곱셈으로 표현할 수 있다.

여기에서 $X^T$는 X를 전치하는 것이고 E는 오차들을 모은 것이다.

행렬을 전치하면 행과 열이 바뀌므로 샘플의 각 특성들을 오차에 곱할 수 있는 형태가 된다.
따라서 X를 전치하였다.

행렬 X는 크기가 (364, 30)에서 전치하면 (30, 364) 크기의 행렬이 된다.
행렬 계산은 (30, 364) $\cdot$ (364, 1) = (30, 1)이 된다.

$g_1$은 모든 샘플의 첫 번째 특성 ($x_1^{(1)}$, $x_1^{(2)}$, …, $x_1^{(364)}$와 오차 ($e^{(1)}$, $e^{(2)}$, …, $e^{(364)}$)를 곱하여 더한 값이므로 이후 gradient 평균값을 계산할때 이 값을 다시 전체 샘플 수로 나눈다.

class SingleLayer:
  def __init__(self, learning_rate = 0.1, l1 = 0, l2 = 0):
    self.w = None
    self.b = None
    self.losses = []
    self.val_losses = []
    self.w_history = []
    self.lr = learning_rate
    self.l1 = l1
    self.l2 = l2
  
  # forpass() 메서드에 배치 경사 하강법을 적용해보자
  def forpass(self, x):
    z = np.dot(x, self.w) + self.b # 행렬 곱셈을 해주는 np.dot()이용하여 선형 출력 계산
    
    return z

  # backprop() 메서드에도 배치 경사 하강법 적용
  def backprop(self, x, err):
    m = len(x)

    # 행렬 곱셈을 적용한 결과가 gradient의 합이기 때문에 전체 샘플 갯수로 나눠 평균 gradient 구함
    w_grad = np.dot(x.T, err) / m # 가중치에 대한 평균 gradient 계산
    b_grad = np.sum(err) / m # 절편에 대한 평균 gradient 계산

    return w_grad, b_grad

  def activation(self, z):
    z = np.clip(z, -100, None)
    a = 1 / (1 + np.exp(-z))

    return a

  # fit() 메서드를 수정해보자
  # 이전에 구현한 SingleLayer 클래스의 fit() 메서드는
  # 에포크를 위한 for문 하나와 훈련 세트를 순회하기 위한 for문 하나로 총 두개의 for문이 있었다.
  # 배치 경사 하강법에서는 forpass() 메서드와 backprop() 메서드에서 전체 샘플을 한꺼번에 계산하므로
  # 두 번째 for문이 삭제된다.
  def fit(self, x, y, epochs = 100, x_val = None, y_val = None):
    y = y.reshape(-1, 1)
    y_val = y_val.reshape(-1, 1)

    # 활성화 출력 a가 열 벡터이므로 이에 맞추어 타깃값을 (m, 1) 크기의 열 벡터로 변환해야 하므로
    # y, y_val 형태를 이에 맞게 변환해줌

    m = len(x)

    self.w = np.ones((x.shape[1], 1))
    self.b = 0
    self.w_history.append(self.w.copy())

    # epochs 만큼 반복
    for i in range(epochs):
      z = self.forpass(x) # 정방향 계산 수행
      
      a = self.activation(z) # 활성화 함수 적용
      
      err = -(y - a) # 오차 계산

      w_grad, b_grad = self.backprop(x, err) # 오차를 역전파하여 gradient 계산

      # gradient에서 패널티 항의 미분값을 더함
      w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m 
      
      # 가중치와 절편을 갱신하자
      self.w -= self.lr * w_grad
      self.b -= self.lr * b_grad

      self.w_history.append(self.w.copy())

      a = np.clip(a, 1e-10, 1-1e-10)

      loss = np.sum(-(y * np.log(a) + (1 - y) * np.log(1 - a))) # 각 샘플의 손실을 더함 -> np.sum()이용
      self.losses.append((loss + self.reg_loss()) / m) # 전체 샘플의 갯수 m 으로 손실의 합을 나눔 -> 평균 손실 구함

      self.update_val_loss(x_val, y_val)

      # 이전에 확률 경사 하강법으로 구현한 것과 비슷하지만 for문이 한 단계 삭제되었기 때문에 코드가 훨씬 간단해졌다.

  def predict(self, x):
    z = self.forpass(x)

    return z > 0

  def score(self, x, y):
    return np.mean(self.predict(x) == y.reshape(-1, 1))

  def reg_loss(self):
    return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w ** 2)

  def update_val_loss(self, x_val, y_val):
    z = self.forpass(x_val)
    a = self.activation(z)
    a = np.clip(a, 1e-10, 1-1e-10)

    # 이전에 fit() 메서드에서 self.losses 구하는 방법과 같다.
    val_loss = np.sum(-(y_val * np.log(a) + (1 - y_val) * np.log(1 - a)))
    self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))

# 훈련 데이터 표준화 전처리를 하자

# 안정적인 학습을 위해 표준화 전처리를 해야한다.
# 사이킷런 StandardScaler 클래스를 사용해 데이터 세트의 특성을 평균이 0, 표준 편차가 1이 되도록 반환하자

# StandardScaler 클래스 이외에도 데이터 전처리 관련된 클래스들은 sklearn.preprocessing 모듈 아래 있다.
# -> 이러한 데이터 전처리 관련 클래스들을 변환기(transformer) 라고 한다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler() # StandardScaler 클래스로 scaler 객체를 만듬
scaler.fit(x_train) # 그 객체(모델)을 fit() 메서드 통해 변환 규칙 익힘

# 훈련 세트와 검증 세트에 표준화를 적용
x_train_scaled = scaler.transform(x_train)
x_val_scaled = scaler.transform(x_val)

# 이 데이터들을 SingleLayer 클래스 객체에 전달하여 배치 경사 하강법을 적용해 보자

single_layer = SingleLayer(l2 = 0.01)
single_layer.fit(x_train_scaled, y_train, x_val = x_val_scaled, y_val = y_val, epochs = 10000)

single_layer.score(x_val_scaled, y_val)

0.978021978021978

score() 메서드에서 출력된 검증 세트의 점수는 저번에 확률적 경사 하강법으로 구현한 SingleLayer 모델과 이번에 배치 경사 하강법으로 구현한(전체 샘플을 사용하여 가중치 업데이트 한) SingleLayer 모델이 같다.

하지만 손실 함수의 변화는 다를 것이다.
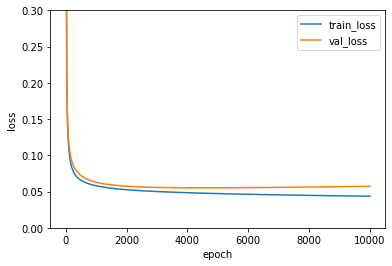
훈련 손실과 검증 손실을 그래프로 출력하여 둘 차이를 비교해보자

plt.ylim(0, 0.3)
plt.plot(single_layer.losses)
plt.plot(single_layer.val_losses)

plt.ylabel('loss')
plt.xlabel('epoch')

plt.legend(['train_loss', 'val_loss'])
plt.show()

# 이전에 확률적 경사 하강법으로 구현한 SingleLayer 클래스의 모듈 경우 손실 그래프의 변동이 매우 심했다.
# 왜냐하면 샘플을 선택하는 순서에 따라 에포크마다 계산된 손실값이 들쭉날쭉했기 때문이다.

# 하지만 이 그래프를 보면 알 수 있듯 배치 경사 하강법을 이용한 경우 전체 샘플을 사용하여 가중치를 업데이트하기 때문에
# 손실값이 안정적을 감소하는 것을 확인할 수 있다.

# 왜 안정적으로 감소하는지 더 자세히 알기 위해 가중치의 변화를 그래프로 나타내보면 알 수 있다.
w2 = []
w3 = []

for w in single_layer.w_history:
  w2.append(w[2])
  w3.append(w[3])

plt.plot(w2, w3)
plt.plot(w2[-1], w3[-1], 'ro')

plt.xlabel('w[2]')
plt.ylabel('w[3]')

plt.show()

# 배치 경사 하강법을 적용하니 가중치를 찾는 경로가 다소 부드러운 곡선의 형태를 나타낸다
# 가중치의 변화가 연속적이므로 당연히 손실값도 안정적으로 수렴될 것이다

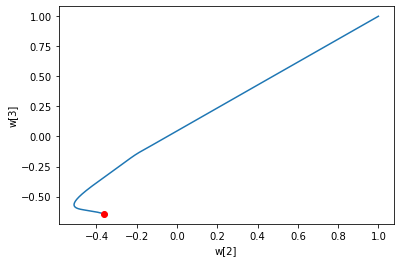
위 그래프를 보니 배치 경사 하강법이 무조건 확률적 경사 하강법 보다 좋다고만 생각할 수도 있다.
물론 여러 면에서 배치 경사 하강법이 좋지만 이전에 언급했듯 매번 전체 훈련 세트를 사용하기 떄문에
연산 비용이 많이 들고 최솟값에 수렴하느 시간도 많이 걸리게 된다는 단점이 존재한다.

이번에는 단일층 신경망에 배치 경사 하강법을 적용하였다.
다음에는 2개의 층을 가진 신경망을 만들어 볼 것이다.

Reference

박해선, 딥러닝 입문, 이지스퍼블리싱, 2019, 149 ~ 155pg

\