수치 예측

11 분 소요

가장 먼저 딥러닝의 기초가 되는 머신러닝 알고리즘 중 가장 간단한 선형회귀를 만들어 볼 것이다.

직선의 그래프 y = ax + b
a : 기울기, b : 절편

선형 회귀(Linear Regression) :

위 선형 방정식의 기울기 a와 절편 b를 찾아내는 방법 즉 선형 방정식(선형 함수)를 예측하는 것
-> 입력 데이터 x와 타깃 데이터 y를 통해 기울기 a와 절편 b를 찾는 것

경사 하강법(Gradient descent) :

위 선형회귀의 목표인 입력 데이터와 타깃 데이터가 주어질 때 그 관계를 잘 표현하는 직선의 방정식(선형 방정식)을 찾아내는 방법
-> 기울기 a, 절편 b를 찾으면 직선의 방정식을 찾을 수 있겠지…
설명이 조금 애매함… 차후 좀더 구체적으로 설명할 것임

경사 하강법은 구체적으로 모델이 데이터를 잘 표현할 수 있도록 기울기(변화율)을 이용하여 모델을 조절하는 방식
-> 즉 기울기를 이용한다는 점!!!! 무슨말인지 이해가 안되면 아래 예제 코드를 이용해 알아보면 된다.

선형 회귀를 푸는 알고리즘은 매우 많은 그 중의 하나가 경사 하강법임!!

from sklearn.datasets import load_diabetes #사이킷런에서 당뇨병 환자 데이터 가져옴
diabetes = load_diabetes()

print(diabetes.data.shape, diabetes.target.shape) # 입력 데이터와 타깃 데이터 크기

(442, 10) (442,)

diabetes.data[0:3] # 당뇨병 환자 데이터 앞부분 3개만

array([[ 0.03807591,  0.05068012,  0.06169621,  0.02187235, -0.0442235 ,
        -0.03482076, -0.04340085, -0.00259226,  0.01990842, -0.01764613],
       [-0.00188202, -0.04464164, -0.05147406, -0.02632783, -0.00844872,
        -0.01916334,  0.07441156, -0.03949338, -0.06832974, -0.09220405],
       [ 0.08529891,  0.05068012,  0.04445121, -0.00567061, -0.04559945,
        -0.03419447, -0.03235593, -0.00259226,  0.00286377, -0.02593034]])

diabetes.target[:3] # 당뇨병 환자 타깃 데이터 앞부분 3개만

array([151.,  75., 141.])

import matplotlib.pyplot as plt
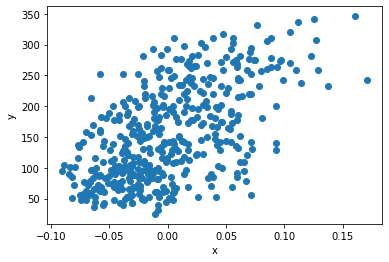
plt.scatter(diabetes.data[:, 2], diabetes.target)
plt.xlabel('x')
plt.ylabel('y')
plt.show() #x축은 입력 데이터, y축은 타깃 데이터로 나타낸 그래프

png

#훈련 데이터 준비
x = diabetes.data[:, 2] #입력 데이터의 세번재 특성 분리하여 x에 저장
y = diabetes.target  #타깃 데이터를 y에 저장

w = 1.0
b = 1.0 # 션형 회귀에서의 가중치(기울기) = w, 절편 = b 를 둘다 1로 임의로 지정

# y = w * x + b 형태

y_hat = x[0]*w + b # 입력 데이터의 첫번째 샘플 x[0]에 대한 예측 데이터 y_hat을 구해본다.
print(y_hat)

1.0616962065186886

print(y[0]) # 첫 번째 샘플 데이터 x[0]에 대응하는 타깃값 y[0]을 출력

151.0

# y[0]과 우리가 예측한 y_hat과 차이가 너무 많이남 -> 우리가 만든 선형 방정식은 현재 데이터에 맞지 않다는 뜻

# w, b를 바꿔야 한다.!! 어떻게 ? y_hat이 y[0]에 비슷해 지도록

w_inc = w + 0.1 # w를 변화시킨 값 w_inc는 w에 0.1을 더한다 (0.1은 아무 의미 x 그냥 더해보는 것)
y_hat_inc = x[0] * w_inc + b # 이번 선형 방정식에 w 대신 w_inc로 바꾼다. 
print(y_hat_inc) # w_inc로 가중치를 바꾸면서 나오게 된 에측 결과를 y_hat_inc

1.0678658271705574

#이전 예측값 y_hat보다 y_hat_inc가 좀더 y[0]에 가까워 지긴 했다.

#w가 0.1 증가하면서 y_hat이 얼마나 변했는지 확인해 보면

w_rate = (y_hat_inc - y_hat) / (w_inc - w) # w_rate는 예측값의 증가 정도를 나타낸다. 
print(w_rate) # 이 w_rate를 훈련 데이터 x[0]에 대한 w의 변화율 이라고 한다.

0.061696206518688734

print(x[0]) # 뭐지 ??? x[0]값과 w_rate(x[0]에 대한 w의 변화율)이 같은 값이다....

# w가 1만큼 증가한다고 가정해보자 그러면 y_hat은 x[0]만큼 증가 할 것 아닌가
# w 변화율 = w가 1만큼 증가할 때 y_hat이 얼만큼 증가하는지에 대한 의미와 같으니
# 당연히 선형 방정식에서는 w 변화율은 x값과 같을 것이다.
# 식으로도 증명 가능 
#w_rate == (y_hat_inc - y_hat) / (w_inc - w) == {(x[0] * w_inc + b) - (x[0] * w + b)} / (w_inc - w)
# = {x[0] * ((w + 0.1) - w)} / ((w + 0.1) - w) = x[0]

0.0616962065186885

# 이제는 가중치(기울기)를 업데이트 하는 방법에 대해 알아보자. (y_hat과 y가 비슷해지게 가중치를 업데이트 하는 방법ㅂ)

w_new = w + w_rate # 기존 가중치에 가중치의 변화율을 더하여 가중치를 업데이트 한다.
print(w_new)

#왜 이런 방법을 ?
# 1. 변화율이 양수일 때 : y_hat이 y에 미치지 못하는 상황에서 변화율이 양수이면 w를 증가 시켜야 y_hat이 증가한다.
# 이때 w의 변화율이 양수이므로 w에 w의 변화율을 더해주면 w는 증가하게 된다.

# 2. 변화율이 음수일 때 : y_hat이 y에 미치지 못하는 상황에서 변화율이 음수이면 w를 감소 시켜야 y_hat이 증가한다.
# 이때 w의 변화율이 음수이므로 w에 w의 변화율을 더해주면 w는 감소하게 된다.

# 즉 변화율이 양수이든 음수이든 w에 w변화율을 더해주면 y_hat이 y에 가까워지는 방향으로 w가 변한다.

1.0616962065186888

# 이전에는 w(가중치)를 변화시켰다면 b(절편)을 변화시켜 보자.
# 절편도 마찬가지 예측값이 타깃값에 가까워지도록 변화시키는 것이 목적!!

b_inc = b + 0.1 # 절편 b에 0.1을 더해보자 (0.1은 아무 의미 없음 그냥 더해보는 것)
y_hat_inc = x[0] * w + b_inc
print(y_hat_inc) # y_hat_inc가 y_hat 보다 y에 가까움

1.1616962065186887

b_rate = (y_hat_inc - y_hat) / (b_inc - b)
print(b_rate) #이번에 b의 변화율에 대해 구해보면 1이 나온다 딱 1!!!!

#선형 방정식에서 b가 1만큼 증가하면 y_hat또한 당연히 1만큼 증가하겠지
#식으로도 증명가능
#b_rate = (y_hat_inc - y_hat) / (b_inc - b) ={} (x[0] * w + b_inc) - (x[0] * w + b)} / (b_inc - b)
# = {(b + 0.1) - b} / {(b + 0.1) - b} = 1

1.0

# w와 마찬가지로 b(절편) 또한 업데이트를 하여 좀 더 타깃값과 유사한 예측값을 내놓게 해야한다.
b_new = b + b_rate # b_rate = 1
# w 업데이트와 같은방법으로 b(절편) 또한 기존 b에 b_rate를 더하여 b를 갱신한다. (b_rate 대신 1로 해도 됨)

'''
위의 방법으로 w, b를 업데이트 한다고 생각해보자
w, b를 변화시켜도 y_hat이 매우 조금 변한다.
이 방법으로는 y와 y_hat의 차이가 매우 큰 경우 y_hat을 y와 유사한 값으로 업데이트 시키는 시간이 매우 오래 걸릴 것 이다.

따라서 위으 문제점을 해결하는 방법으로 "오차 역전파"를 이용한다.

오차 역전파 (backpropagation)
'''

err = y[0] - y_hat # 에러 값을 구한다. 에러값(오차) = 실제 값 - 예측값 
'''
오차 역전파 : 
이전에 w, b를 갱신할때 w에는 w_rate를 더해주고, b에는 b_rate를 더해줬음
하지만 오차 역전파 방법은 y와 y_hat의 차이를 이용하여 w와 b를 업데이트 한다.
-> 오차가 연이어 전파되는 모습으로 수행

w에 w_rate * 에러값, b에는 b_rate * 에러값 을 더해주는 방식으로 w와 b를 갱신한다.
'''

w_new = w + w_rate * err # 일단 처음에 x[0]일때 w의 변화율과 b의 변화율에 오차를 곱하여 w변화율과 b변화율을 갱신
b_new = b + b_rate * err  

print(w_new, b_new) # -> 이전에 오차를 이용하지 않은 방법에 비해 w변화율과 b변화율이 매우 크게 변했음

911.1983904448475 156.2427820067777

y_hat = x[1] * w_new + b_new # 위 방식대로 x[1]에 대해
err = y[1] - y_hat
w_rate = x[1]
b_rate = 1 
w_new = w_new + w_rate * err
b_new = b_new + b_rate * err
print(w_new, b_new)

14.132317616381767 75.52764127612664

# x[0], x[1]을 이용해 w, b를 갱신하였다. 하지만 모든 입력 샘플에 대해 적용하여 w, b를 갱신하자
# 많이 할수록 w, b가 실제 데이터 타겟에 맞게 갱신되지 않을까?
for x_i, y_i in zip(x, y):
  y_hat = x_i * w + b

  err = y_i - y_hat

  w_rate = x_i
  w = w + w_rate * err

  b_rate = 1
  b = b + b_rate * err

print(w, b)

587.8654539985689 99.40935564531424

'''
위 방식으로 갱신한 w, b를 이용해 선형함수가 과연 실제 입력 x에 대한 타깃 y를 잘 예측할지 
그래프에 나타내 보자.

산점도 -> 입력 x값에 대한 실제 타깃 y값

직선 -> 우리가 구해본 선형 함수(y = w * x + b) 
'''
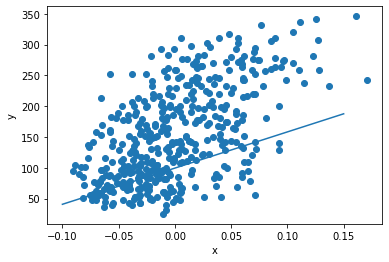
plt.scatter(x, y)
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)

plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()

#먼가 아쉬움.... 직선이 실제 입력과 타깃과의 관계를 정확히 나타내지는 못하는 것 같음..

png

'''
어떻게 하면 좀더 입력에 대한 실제 타깃과의 관계를 정확히 타나내는 선형 방정식을 구할 수 있을까/
즉 더 적합한 w, b를 구할 수 있을까?

보통 경사 하강법은 주어진 trainning data로 학습을 여러 번 반복함 
이전 까지는 한번만 반복햇음... -> 적합한 w, b를 찾는데 학습량이 부족했음..

에포크(epoch) : 이렇게 전체 훈련데이터를 모두 이용하여 한 단위 작업을 진행하는 것
'''
for i in range(0, 100): #100번의 에포크 진행해 보자!!!
  for x_i, y_i in zip(x, y):
    y_hat = x_i * w + b
    err = y_i - y_hat

    w_rate = x_i
    w = w + w_rate * err

    b_rate = 1
    b = b + b_rate * err

print(w, b) #100번의 에포크를 진행하고 난 뒤의 갱신된 w, b가 이전과 달라져 있음

913.5973364345905 123.39414383177204

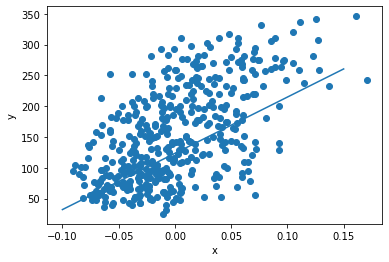
#에포크 100번 진행한 뒤의 갱신된 w, b가 실제 x와 타깃 y의 관계를 잘 나타내는 선형방정식을 보이는지
#그래프를 통해 보자.

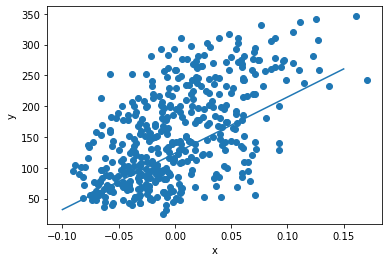
plt.scatter(x, y) 
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()

#에포크 1번 보다 훨씬 실제 데이터의 입력과 타깃 관계를 잘 나타내는 선형 방정식을 보인다.
#즉 에포크를 늘리니 더 적합한 w, b를 갱신할 수 있다는 것을 알게 되었다.

png

x_new = 0.18 #그러면 이전에 구한 갱신된 w, b로 구한 선형방정식으로 새로운 입력 x에 대한 타깃 y를 예측해 보자.
y_pred = x_new * w + b
print(y_pred)

287.8416643899983

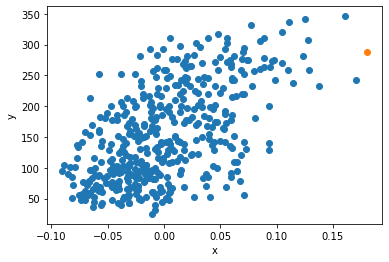
plt.scatter(x, y) 
plt.scatter(x_new, y_pred) #새로운 입력 x에 대해 갱신된 w, b로 구한 선형방정식으로 예측한 y를 그래프에 나타내 보자.
plt.xlabel('x')
plt.ylabel('y')
plt.show()

# 주황색? 으로 나타난 점이 새로운 입력 x에 대한 예측 y 값이다.. 실제 데이터 산점도에 어색하지 않은 위치인 것을 보니 괜찮게 예측한 것 같다..

png

이전에 정의한 경사 하강법은 조금 애매한 설명…. 다시 설명하자면

경사 하강법(Gradient descent) :

손실 함수가 정의되었을 때 손실 함수의 값이 최소가 되는 지점 찾는 방법

손실함수가 뭔데???…

손실 함수(loss function) = 비용 함수(cost function) = 목적 함수(objective function):

예상한 값과 실제 타깃값의 차이를 함수로 정의한 것

앞에서 적합한 가중치와 절편을 찾기 위해 사용한 경사 하강법에서 쓰인 손실 함수는 무엇일까?
바로 제곱 오차라는 손실 함수이다.

제곱 오차(Squared error) : SE = (y-y_hat)$^2$

타깃 값에서 예측 값을 뺀 후 제곱한 값

앞에서는 제곱 오차라는 손실 함수를 미분하여 가중치와 절편을 갱신하엿음..

미분????

이 부분을 알기 위해 제곱 오차라는 손실 함수를 파해쳐 보자

위에서 경사하강법이 곧 손실 함수의 값이 최소가 되는 지점을 찾는 방법 이라고 하였다.
그러면 최솟값을 어떻게 찾지???

아니 아까 예제 코드에서 w(가중치)와 b(절편)값 조절 하면서 y_hat 구했잖아….
y_hat과 y의 차이 즉 예측값과 실제 타깃 값 차이가 적으면 제곱 오차 함수 값도 작겠네 y- y_hat의 제곱이 작아질 테니…

아무튼 우리 w, b 갱신할 때 w_rate, b_rate 구하던거 기억날 것임.. 즉 가중치 변화량과 절편 변화량을 이용하여 w, b 갱신했잖아..

이 방법과 유사한 방식으로 w_rate(가중치 변화량), b_rate(절편 변화량) 구하는 것과 유사하게 가중치에 대한 손실 함수의 변화율과 절편에 대한 손실 함수의 변화율로 가중치와 절편을 갱신할 것이다.

구체적인 방법은 아래에서 설명

가중치에 대한 손실 함수에 (여기선 제곱 오차 함수) 변화량을 구하기 위해서 손실 함수에 가중치에 대해 미분을, 절편에 대한 손실 함수의 변화량 구하기 위해선 손실 함수에 절편에 대해 미분을 해주는 것이다.

자 다시!! 제곱 오차 함수의 최솟값을 얻기 위해 … 가중치에 대해 미분과 절편에 대해 미분을 해보자..

가중치에 대한 제곱 오차 미분을 하자

제곱 오차 식에 가중치(w)에 대해 편미분하면

$\frac{\delta SE}{\delta w} = \frac{\delta}{\delta w}(y - $y_hat$)^2 = 2(y -$ y_hat$)(-\frac{\delta}{\delta w}$y_hat$) = 2(y - $y_hat$)(-x) = -2(y - $y_hat$)x$

정리하면 $\frac{\delta SE}{\delta w} = -2(y - $y_hat$)x$

만약에 처음에 제곱 오차 공식을 (y-y_hat)$^2$가 아닌 2(y-y_hat)$^2$였다면 미분시 2와 $\frac{1}{2}$이 곱해지면서 1이 되어 훨씬 깔끔하게 표현 되었을 것이다. 따라서 보통은 제곱 오차 공식을 2로 나눈 함수를 편미분 하여

$\frac{\delta SE}{\delta w} = -(y - $y_hat$)x$

이와 같은 방식으로 나타내기도 한다. 앞으로는 이렇게 나타낼 것임

이제는 가중치에 대한 제곱 오차 함수의 변화율을 구하였으니 이전 예제 코드에서 가중치 갱신에 변화율을 더했던 방법과 비슷한 방법으로 가중치를 갱신할 것이다.
이 방법에서는 기존 w에서 변화율을 뺄 것이다.

이전 예제 코드와 다르게 왜 여기선 w에서 변화율을 더하지 않고 빼냐??

-> 손실 함수의 낮은 쪽으로 이동하기 위해서

아니 무슨말 ??
이전에는 단순히 예측값이 기존 타깃값보다 작았기 때문에 예측값을 크게해주기 위해 가중치나 절편을 늘려야 했기 때문에 가중치와 절편에 각자의 변화율을 더해준 것 이라면 지금은 손실함수를 적용하였음
손실함수의 최솟값을 구하는 것이 곧 예측값과 타깃값을 유사하게 만드는 것이니 손실함수값을 낮추기 위해 가중치와 절편에 손실 함수에 대한 각자의 변화율을 빼주는 것이다. !!!

w = w - $\frac{\delta SE}{\delta w}$ = w + (y - y_hat)x

위 식은 이전 예제 코드에서 오파 역전파를 알아보면서 보았던 식임…. (w + w_rate * err)
(y - y_hat)이 err고 err에 w_rate곱한 값에 기존 w를 더하여 갱신된 w를 만든다.

가중치와 마찬가지로 절편에 대하여 제곱 오차 미분을 하면

제곱 오차 식에 절편(b)에 대해 편미분하면

$\frac{\delta SE}{\delta b} = \frac{\delta}{\delta b}\frac{1}{2}(y - $y_hat$)^2 = (y -$ y_hat$)(-\frac{\delta}{\delta b}$y_hat$) = (y - $y_hat$)(-(b - $b_hat$)) = (y - $y_hat$)(-1) = -(y - $y_hat$)1$

b - b_hat = 1 인 것은 이전에 설명 하였으니 이해가 될 것이다

정리 하면 $\frac{\delta SE}{\delta b} = -(y - $y_hat)

가중치에서 가중치에 대한 제곱 오차 함수의 변화율을 뺀 방식과 유사하게 절편에서 절편에 대한 제곱 오차 함수의 변화율을 빼면

b = b - $\frac{\delta SE}{\delta b} = b + (y - $y_hat)

이제부터 손실 함수에 대해 일일이 변화율의 값을 계산하는 대신 편미분 이용하여 변화율 계산할 것임…

변화율 = Gradient

'''
위에서 경사 하강법을 이용하여 회귀 문제를 변화율을 직접 구하는 방식, 편미분을 이용한 방식(손실 함수) 두 가지 방식을 이용하였다.
아래 예제는 두 가지 방법 모두 사용한 방식으로 파이선 클래스를 만들어 볼 것임
'''
class Neuron:
  def __init__(self):
    self.w = 1.0
    self.b = 1.0

  def forpass(self, x): #정방향 계산을 위한 메서드 정의
    y_hat = x * self.w + self.b

    return y_hat

  #정방향 계산 : 뉴런으로 도식화한 상태에서 y_hat을 구하는 방향으로의 계산

  def backprop(self, x, err): #역방향 계산을 위한 메서드 정의 
    w_rate = x  
    b_rate = 1

    w_grad = w_rate * err  #이전에 설명한 경사 하강법 이용
    b_grad = b_rate * err

    return w_grad, b_grad

  #역방향 계산 : 이전에 계산한 y_hat으로 정방향 계산과 반대로 y_hat과 y의 오차를 이용해 w와 b를 갱신
  # 즉 정방향 계산과 반대의 방향으로 계산되는 것을 알 수 있다. 
  #따라서 오차역전파(backpropagation)이라는 용어가 나오게 된 것!!!!!

  def fit(self, x, y, epochs = 100): #훈련을 위한 메서드 구현
    for i in range(epochs):
      for x_i, y_i in zip(x, y):
        y_hat = self.forpass(x_i) #forpass 메서드 이용해 y_hat구함
        
        err = -(y_i - y_hat) #타깃값과 예측값의 오차를 구함

        w_grad, b_grad = self.backprop(x_i, err) #backprop 메서드를 이용해 w, b를 갱신

        self.w -= w_grad
        self.b -= b_grad

neuron = Neuron() #위에서 만든 클래스에 대한 객체를 만들고
neuron.fit(x, y) # 만든 객체를 이용해 입력 data x 와 타깃 data y를 전달하여 훈련함

# 학습이 완료된 결과 (w, b를 이용한 선형 함수)를 그래프에 나타내 보자
plt.scatter(x, y)
pt1 = (-0.1, -0.1 * neuron.w + neuron.b)
pt2 = (0.15, 0.15 * neuron.w + neuron.b)

plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])

plt.xlabel('x')
plt.ylabel('y')

plt.show()

png

Reference

박해선, 딥러닝 입문, 이지스퍼블리싱, 2019, 45~74pg

Twitter Facebook LinkedIn

Jo Jaecheol

수치 예측

선형 회귀(Linear Regression) :

경사 하강법(Gradient descent) :

경사 하강법(Gradient descent) :

손실 함수(loss function) = 비용 함수(cost function) = 목적 함수(objective function):

제곱 오차(Squared error) : SE = (y-y_hat)$^2$

미분????

아무튼 우리 w, b 갱신할 때 w_rate, b_rate 구하던거 기억날 것임.. 즉 가중치 변화량과 절편 변화량을 이용하여 w, b 갱신했잖아..

이 방법과 유사한 방식으로 w_rate(가중치 변화량), b_rate(절편 변화량) 구하는 것과 유사하게 가중치에 대한 손실 함수의 변화율과 절편에 대한 손실 함수의 변화율로 가중치와 절편을 갱신할 것이다.

가중치에 대한 손실 함수에 (여기선 제곱 오차 함수) 변화량을 구하기 위해서 손실 함수에 가중치에 대해 미분을, 절편에 대한 손실 함수의 변화량 구하기 위해선 손실 함수에 절편에 대해 미분을 해주는 것이다.

가중치에 대한 제곱 오차 미분을 하자

$\frac{\delta SE}{\delta w} = \frac{\delta}{\delta w}(y - $y_hat$)^2 = 2(y -$ y_hat$)(-\frac{\delta}{\delta w}$y_hat$) = 2(y - $y_hat$)(-x) = -2(y - $y_hat$)x$

정리하면 $\frac{\delta SE}{\delta w} = -2(y - $y_hat$)x$

$\frac{\delta SE}{\delta w} = -(y - $y_hat$)x$

이전 예제 코드와 다르게 왜 여기선 w에서 변화율을 더하지 않고 빼냐??

-> 손실 함수의 낮은 쪽으로 이동하기 위해서

w = w - $\frac{\delta SE}{\delta w}$ = w + (y - y_hat)x

가중치와 마찬가지로 절편에 대하여 제곱 오차 미분을 하면

$\frac{\delta SE}{\delta b} = \frac{\delta}{\delta b}\frac{1}{2}(y - $y_hat$)^2 = (y -$ y_hat$)(-\frac{\delta}{\delta b}$y_hat$) = (y - $y_hat$)(-(b - $b_hat$)) = (y - $y_hat$)(-1) = -(y - $y_hat$)1$

정리 하면 $\frac{\delta SE}{\delta b} = -(y - $y_hat)

b = b - $\frac{\delta SE}{\delta b} = b + (y - $y_hat)

변화율 = Gradient

Reference

공유하기

참고

회원 도메인 개발

애플리케이션 구현 준비

엔티티 설계시 주의점

도메인 분석 설계