과대 적합, 과소 적합
과대 적합(overfitting), 과소 적합(underfitting) 개념에 대해 알아보고자 한다.
훈련 세트와 검증 세트는 모델의 과대 적합과 과소 적합 이라는 문제와 매우 깊게 연관 되어 있다.
학습 곡선을 통해 과대적합과 과소적합에 대해 알아보자
과대 적합(Overfitting) :
모델이 훈련 세트에서는 좋은 성능을 내지만 검증 세트에서는 낮은 성능을 내는 경우
과소 적합(Underfitting) :
훈련 세트와 검증 세트의 성능에는 차이가 크지 않지만 모두 낮은 성능을 내는 경우
훈련 세트의 크기와 과대 적합과 과소 적합 분석을 해보자
훈련 세트의 크기에 따라 과대 적합과 과소 적합이 어떻게 나타나는지 그래프를 통해 알아보자
위와 같은 그래프를 학습 곡선(Learning curve) 이라 부른다.
첫 번재 학습 곡선은 과대 적합의 전형적인 모습으로 훈련 세트와 검증 세트에서 측정한 성능간의 간격이 큰 경우이다.
따라서 과대 적합된 모델을 분산이 크다(high variance) 라고 말한다.
과대 적합의 주요 원인 중 하나는 훈련 세트에 충분한 다양한 패턴의 샘플이 없는 경우이다.
다양한 패턴의 샘플이 없는것이 왜 과대 적합을 일으키지 ??
훈련 세트에 다양한 패턴이 없다면 검증 세트에 제대로 적응하지 못할 것이기 때문이다.
이런 경우에는 더 많은 훈련 샘플을 추가하여 검증 세트의 성능을 향상 시킬 수 있다.
만약 훈련 샘플을 더이상 모을 수 없는 경우라면 모델이 훈련 세트에 집착하지 않도록 가중치를 제한할 수 있다.
이 방법을 모델의 복잡도를 낮춘다 라고 표현을 한다.
(모델의 복잡도를 낮추는 방법은 추후에 알아보자)
두 번째 학습 곡선은 전형적인 과소 적합의 모습으로 훈련 세트와 검증 세트에서 측정한 성능의 간격은 훈련 세트의 크기가 커질수록 점점 더 가까워 지지만 훈련세트, 검증세트 모두 정확도가 떨어진다(성능이 떨어진다)
따라서 과소적합된 모델을 편향이 크다(high bias)
과소 적합의 주요 원인 중 하나는 모델이 충분히 복잡하지 않아 훈련 데이터에 있는 패턴을 모두 잡아내지 못하는 현상이다.
위 원인으로 인한 과소 적합을 해결하는 대표적인 방법은 복잡도가 더 높은 모델을 사용하거나 가중치의 규제를 완화하는 방법이다.
세 번째 학습 곡선은 과대적합과 과소적합 사이에서 절충점을 찾은 것이다.
에포크와 손실 함수의 그래프로 과대 적합과 과소 적합을 분석해보자
이전에 배운 에포크에 대한 손실 함수의 그래프를 사용하여 과대 적합과 과소 적합울 분석하기도 한다.
따라서 에포크에 대한 손실 함수의 그래프를 학습 곡선이라고 부르는 경우가 종종 있다.
위 그래프는 에포크와 손실 함수에 대한 그래프와 에포크와 정확도에 대한 그래프 이다
이 그래프 들을 통해 과대 적합과 과소 적합에 대해 알아볼 것이다.
왼쪽 그래프를 보면 훈련 세트의 손실은 에포크가 진행될 수록 감소하지만 검증 세트의 손실은 에포크의 횟수가 최적점을 지나면 오히려 상승하는 것을 확인할 수 있다
에포크가 늘면 늘수록 손실은 줄어야 하는것 아닌가???
-> 최적점 이후에도 계속해서 훈련 세트로 모델을 학습시키면 모델이 훈련 세트의 샘플에 대해 더 밀착하여 학습하기 때문에 훈련 세트에만 너무 맞는 모델이 되어버리기 때문이다.
즉 최적점 이후부터 계속 학습을 하면 모델이 과대 적합하기 시작한다는 뜻이다.
반대로 최적점 이전에는 훈련 세트와 검증 세트의 손실이 비슷한 간격을 유지하면서 함께 줄어드는 것을 볼 수 있는데 아 영역에서 학습을 중단하면 (최적점 전에 학습을 중단) 과소 적합된 모델이 만들어 진다.
오른쪽 그래프는 세로축에 손실 대신 정확도를 사용했으니 왼쪽 그래프가 뒤집혀진 결과와 같다.
모델 복잡도와 손실 함수의 그래프로 과대 적합과 과소 적합을 분석해보자
위 그래프 처럼 학습 곡선 그래프를 가로 추겡 에포크 대신 모델 복잡도를 넣어 그래프를 표현하기도 한다.
모델 복잡도가 뭐지 ??
모델 목잡도 :
모델이 가진 학습 가능한 가중치 개수를 말한다. 층의 개수나 유닛의 개수가 많아지면 복잡도가 높은 모델이 된다.
모델이 복잡해지면 좋을 것 같은데 꼭 그렇지 많은 않다. 아니 너무 복잡해지면 오히려 좋지 않다.
예를 들어서 모델이 훈련 세트에만 잘 맞는 형태로 만들어 지면 훈련 세트에서만 좋은 성능을 만들기 때문에 좋은 성능을 내기 때문이다 -> 이러한 경우가 과대적합이다.
자 지금까지 다양한 학습 곡선을 통해 과대 적합과 과소 적합에 대해 알아 보았는데
정리해보면 좋은 성능을 내는 모델을 만들기 위해 여러 조건이 필요함을 알 수 있다.
특히 에포크 횟수에 따라 최적점을 기준으로 오히려 에포크 횟수가 더 커지면 과대 적합, 에포크 횟수가 더 적으면 과소 적합이 되었던 것을 알게 되었다.
그럼 적절한 에포크 횟수에 대해 알아보자
적절한 편향 - 분산 트레이드오프를 선택하자
편향 - 분산 트레이드오프가 뭐야 ??
이것을 설명하기 이전에 과소 적합된 모델은 편향 되었다라고 하고 과대 적합된 모델은 분산이 크다 라고 하였다.
편향 - 분산 트레이드오프(bias-variance tradeoff) :
과소 적합된 모델(편향)과 과대 적합된 모델(분산) 사이의 관계
트레이드 오프라는 말이 들어가게 된 이유는 하나를 얻기 위해 다른 하나를 희생해야 하기 때문이다.
편향 - 분산 트레이드오프란 편향을 줄이면(훈련 세트의 성능을 높이면) 분산이 커지고(검증 세트와 성능 차이가 커지고) 반대로 분산을 줄이면(검증 세트와 성능 차이를 줄이면) 편향이 커지는(훈련 세트의 성능이 낮아진다는) 것을 말한다.
따라서 분산이나 편향이 너무 커지지 않도록 적절한 중간 지점을 찾아야 한다.
이러한 행위를 적절한 편향 - 분산 트레이드오프를 선택했다
이제부터 경사하강법의 에포크 횟수에 대한 모델의 손실을 그래프로 그려 ‘적절한 편향-분산 트레이드오프’를 선택해 보자.
# 검증 손실을 기록하기 위한 변수 추가하기
# 훈련 세트의 손실을 기록했듯이 검증 세트에 대한 손실을 기록한 다음 기록한 값으로 그래프를 그려볼 것이다.
# 이를 위해 SingleLayer 클래스의 __init__() 메서드에 self.val_losses 인스턴스 변수를 추가해보자
# 가중치를 기록할 변수와 학습률 파라미터 추가해보자
import numpy as np
class SingleLayer:
def __init__(self, learning_rate = 0.1):
self.w = None
self.b = None
self.losses = []
self.val_losses = [] # self.val_losses 변수 추가 !!
self.w_history = []
self.lr = learning_rate
self.losses = []
def forpass(self, x):
z = np.sum(x * self.w) + self.b
return z
def backprop(self, x, err):
w_grad = x * err
b_grad = 1 * err
return w_grad, b_grad
def activation(self, z):
z = np.clip(z, -100, None)
a = 1 / (1 + np.exp(-z))
return a
def fit(self, x, y, epochs = 100, x_val = None, y_val = None): # x_val, y_val 매개변수 추가
self.w = np.ones(x.shape[1])
self.b = 0
self.w_history.append(self.w.copy())
np.random.seed(42)
for i in range (epochs):
loss = 0
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes:
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backprop(x[i], err)
self.w -= self.lr * w_grad
self.b -= b_grad
self.w_history.append(self.w.copy())
a = np.clip(a, 1e-10, 1 - 1e-10)
loss += -(y[i] * np.log(a) + (1 - y[i]) * np.log(1 - a))
self.losses.append(loss/len(y))
self.update_val_loss(x_val, y_val) # 검증 세트에 대한 손실을 계산
def predict(self, x):
z = [self.forpass(x_i) for x_i in x]
return np.array(z) > 0
def score(self, x, y):
return np.mean(self.predict(x) == y)
# 검증 손실 계산하자
def update_val_loss(self, x_val, y_val):
if x_val is None:
return
val_loss = 0
for i in range(len(x_val)):
z = self.forpass(x_val[i]) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
a = np.clip(a, 1e-10, 1 - 1e-10)
val_loss += -(y_val[i] * np.log(a) + (1 - y_val[i]) * np.log(1 - a))
self.val_losses.append(val_loss / len(y_val))
# 이 계산은 fit() 메서드에서 훈련 세트의 손실을 계산하는 방식과 동일
# 검정 세트 샘플을 정방향으로 계산하고 활성화 함수를 통과시켜 출력값 계산한다
# 이 값을 이용해 로지스틱 손실 함수의 값을 계산 위해 val_losses 리스트에 추가함
# 검증 세트에 대한 손실 함수 값을 계산위해 fit() 메서드에서 epoch 1번 마다 update_val_loss() 메서드 호출
# 모델을 훈련해 보자
# 데이터 세트를 준비한다
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
x = cancer.data
y = cancer.target
x_train_all, x_test, y_train_all, y_test = train_test_split(x, y, stratify = y, test_size = 0.2, random_state = 42)
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify = y_train_all, test_size = 0.2, random_state = 42)
train_mean = np.mean(x_train, axis = 0)
train_std = np.std(x_train, axis = 0)
x_train_scaled = (x_train - train_mean) / train_std
val_mean = np.mean(x_val, axis = 0)
val_std = np.std(x_val, axis = 0)
x_val_scaled = (x_val - val_mean) / val_std
layer3 = SingleLayer()
layer3.fit(x_train_scaled, y_train, x_val = x_val_scaled, y_val = y_val)
# 손실값으로 그래프를 그려 에포크 횟수를 지정하자
# fit() 메서드를 수정하여 에포크마다 훈련 세트와 검증 세트의 손실값을 인스턴스 변수 self.val_losses에 저장하도록 만들었다.
# 이 값을 이용해 그래프를 그려보자
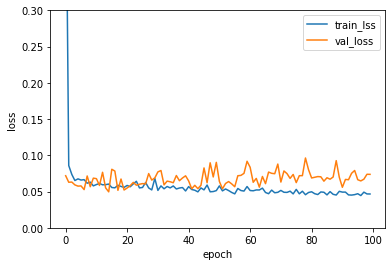
import matplotlib.pyplot as plt
plt.ylim(0, 0.3)
plt.plot(layer3.losses)
plt.plot(layer3.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_lss', 'val_loss'])
plt.show()
# 그래프를 보면 검증 손실이 대략 epoch 20번째 이후에 훈련 세트보다 높아지는 것을 알 수 있다.
# 즉 epoch가 진행됨에 따라 가중치는 훈련 세트에 잘 맞게 되지만 검증 세트에는 잘 맞지 않게 되는 것이다.
# 그 절충점이 epoch 20번째 쯤으로 보인다.
# 그럼 적절한 절충점인 epoch 횟수에서 훈련을 종료하고 싶기 때문에
# 훈련을 조기 종료 하도록 해보자
# 이렇게 훈련을 일찍 끝내는 방법을 조기 종료(early stopping) 이라고 부른다.
layer4 = SingleLayer()
layer4.fit(x_train_scaled, y_train, epochs = 20)
layer4.score(x_val_scaled, y_val)
# 이전 스케일 조정 한 이후에 정확도가 0.967 정도엿는데 그에 비해 정확도가 확실히 올랐음을 확인할 수 있다.
# 그 이유는 과대 적합되기 이전에 훈련을 멈추었기 떄문에 가능했다.
0.978021978021978
과대 적합, 과소 적합에 대해 알아 보았다.
이후에는 이전에 설명한 과대 적합을 해결하는 대표적인 방법 중 하나인 가중치 규제 방법에 대해 좀더 자세히 알아 보고자 한다.
Reference
박해선, 딥러닝 입문, 이지스퍼블리싱, 2019, 131 ~ 136pg